PENGERTAN DAN JENIS-JENIS MATRIKS
Matriks adalah kumpulan bilangan yang disusun dalam
bentuk baris dan kolom. Bilangan yang tersusun dalam baris dan kolom
disebut elemen matriks. Nama matriks ditulis dengan menggunakan huruf
kapital.
Banyaknya baris dan kolom matriks disebut ordo matriks.
Bentuk umum:
- Matriks baris adalah matriks yang hanya memiliki satu baris. Contoh : A = [ 2 3 0 7 ]
- Matriks kolom adalah matriks yang hanya memiliki satu kolom. Contoh :

- Matriks persegi adalah matriks yang jumlah kolomnya sama. Contoh:

- Matriks Identitas adalah matriks persegi yang elemen-elemen pada diagonal utamanya1, sedangkan semua elemen yang lainnya nol. Contoh:

- Matriks Segitiga Atas adalah matriks persegi yang elemen-elemen dibawah diagonal utamanya nol. Contoh:

- Matriks Segitiga Bawah adalah matriks persegi yang elemen-elemen diatas diagonal utamanya nol. Contoh:
 Matriks Nol adalah matriks yang semua elemennya nol. Contoh:
Matriks Nol adalah matriks yang semua elemennya nol. Contoh: 
Pada matriks dikenal beberapa jenis operasi seperti penjumlahan, pengurangan, dan
perkalian. Dalam masing-masing operasi tersebut punya karakteristik sendiri-sendiri. Berikut selengkapnya:
1. penjumlahan Matriks
Penjumlahan matriks hanya dapat dilakukan terhadap matriks-matriks
yang mempunyai ukuran (orde) yang sama. Jika A=(aij) dan B=(bij) adalah
matriks-matriks berukuran sama, maka A+B adalah suatu matriks C=(cij)
dimana (cij) = (aij)+(bij) atau [A]+[B] = [C] mempunyai ukuran yang sama
dan elemennya (cij) = (aij) + (bij)
Contoh:

A+C tidak terdefinisi (tidak dapat dicari hasilnya) karena matriks A dan matriks B mempunyai ukuran yang berbeda
2. Pengurangan Matriks
Sama seperti pada penjumlahan matriks, pengurangan matriks hanya
dapat dilakukan pada matriks-matriks yang mempunyai ukuran yang sama.
Jika ukurannya berbeda maka matriks hasil tidak terdefinisikan.
Contoh:
 3. Perkalian Matriks dengan Skalar
3. Perkalian Matriks dengan Skalar
Jika k adalah suatu bilangan skalar dan A=(aij) maka matriks kA(kaij)
yaitu suatu matriks kA yang diperoleh dengan mengalikan semua elemen
matriks A dengan k. Mengalikan matriks dengan skalar dapat dituliskan di
depan atau dibelakang matriks. Misalnya [C]=k[A]=[A]k dan (c
ij ) = (ka
ij )
Pada perkalian matriks dengan skalar berlaku hukum distributif dimana k(A+B)=kA+kB
Contoh:
 4. Perkalian Matriks dengan Matriks
4. Perkalian Matriks dengan Matriks
Beberapa hal yang harus diperhatikan:
- Perkalian matriks dengan matriks umumnya tidak komutatif
- Syarat perkalian adalah jumlah banyaknya kolom pertama matriks sama dengan jumlah banyaknya baris matriks kedua
- Jika matriks A berukuran mxp dan matriks pxn maka perkalian A*B adalah suatu matriks C=(cij) berukuran mxn dimana
Contoh:
 5. Transpose Matriks
5. Transpose Matriks
Transpose dari suatu matriks merupakan pengubahan baris menjadi kolom
dan kolom menjadi baris. Transpos dari matrik A dinotasikan A
T.
Jadi mirip transpose yang ada di excel. Jika sebuah matriks berordo 3 x
4 ketika ditransporse akan menjadi matriks berorde 4 x 3. contoh:

Dalam matriks dikenal istilah matriks simetri, yaitu matriks yang ketika ditranspose sama dengan sebelum ditranspos. Contoh:

Karena A = At maka A disebut matriks simetri.
6. Determinan Matriks
Setiap matriks bujur sangkar mempunyai nilai
determinan. Nilai determinan dari suatu matriks merupakan suatu skalar.
Jika nilai determinan suatu matriks sama dengan nol, maka matrik
tersebut disebut matriks singular. Matriks singular tidak mempunyai
invers/ balikan.
Determinan dari matriks-matriks khusus:
(a) Matriks Diagonal

(b) Matriks Segitiga Atas

(c) Matriks Segitiga Bawah
 7. Invers Matriks
7. Invers Matriks
Invers hanya dipunyai oleh matriks yang tidak singuler. Invers matriks A dinyatakan dengan A
-1 dan secara umum dirumuskan:







 tentukan determinan A
tentukan determinan A = detM = a22a33 - a23a32
= detM = a22a33 - a23a32
 = detM = a11a23 - a13a21
= detM = a11a23 - a13a21 tentukan determinan A dengan metode Minor dan kofaktor
tentukan determinan A dengan metode Minor dan kofaktor = 1 (-3) = -3
= 1 (-3) = -3 = -1 (-8) = 8
= -1 (-8) = 8 = 1 (-7) = -7
= 1 (-7) = -7 + a13
+ a13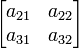
 + 3
+ 3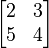 = 1(-3) - 4(-4) + 3(-7) = -8
= 1(-3) - 4(-4) + 3(-7) = -8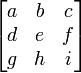 tentukan determinan A
tentukan determinan A = (1x5x1 + 2x4x3 + 3x4x2) - (3x5x3 + 2x4x1 + 1x4x2) = 53 - 61 = -8
= (1x5x1 + 2x4x3 + 3x4x2) - (3x5x3 + 2x4x1 + 1x4x2) = 53 - 61 = -8















